Julia Gygax

Julia Gygax

PhD Student in Computational Neuroscience in the Zenke Lab at FMI Basel, Switzerland

Publications

Elucidating the Theoretical Underpinnings of Surrogate Gradient Learning in Spiking Neural Networks

Gygax, Julia & Zenke, Friedemann.
Neural Computation, 2025

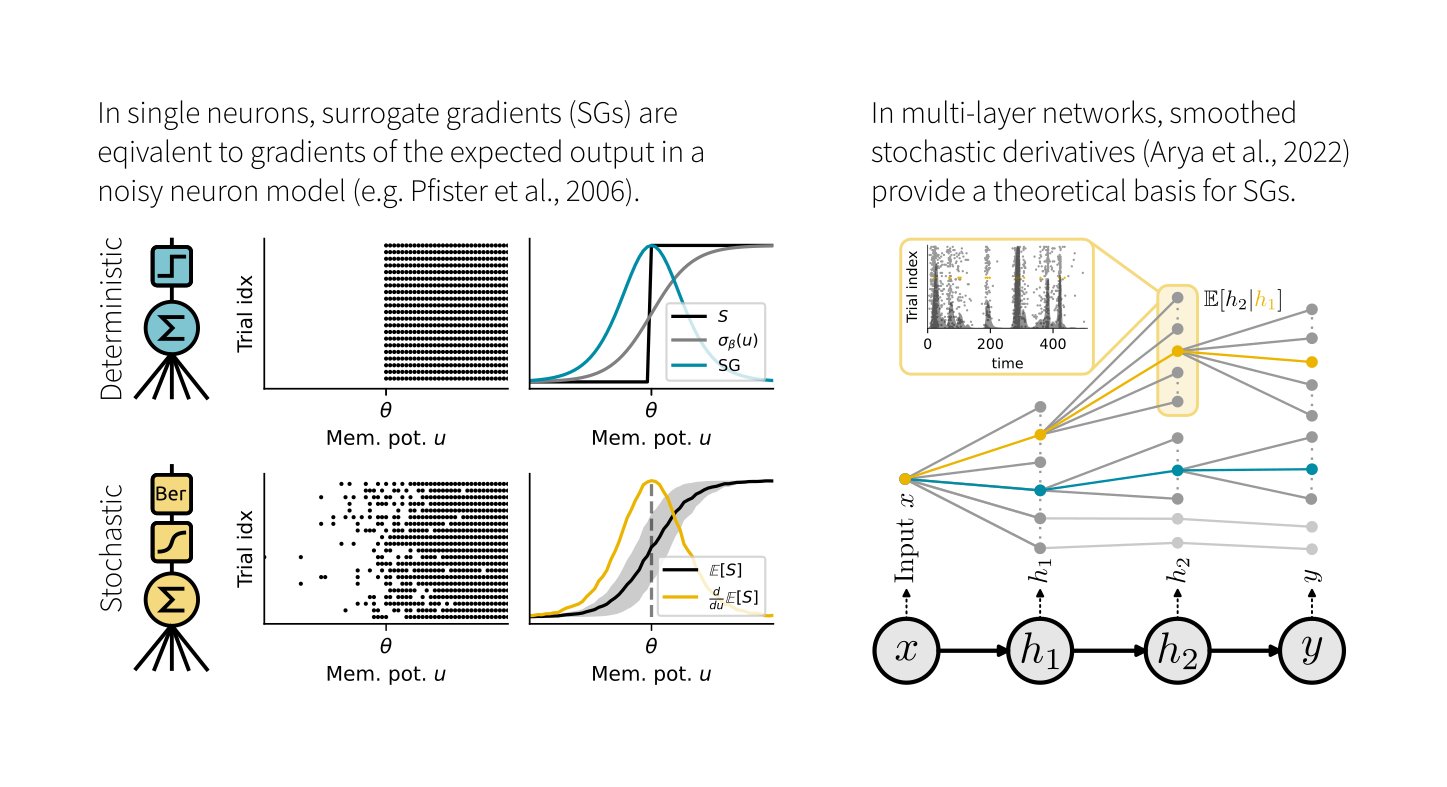
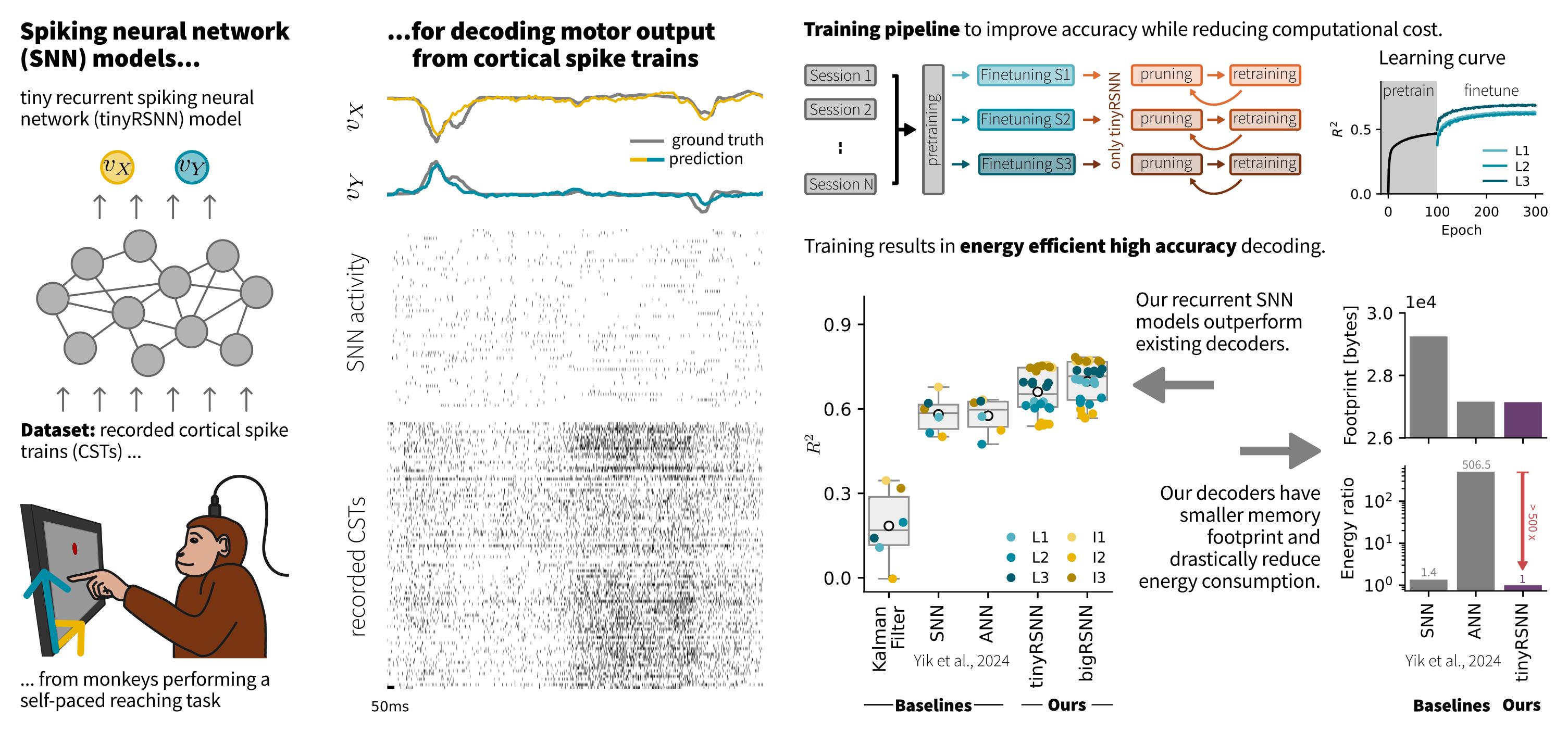
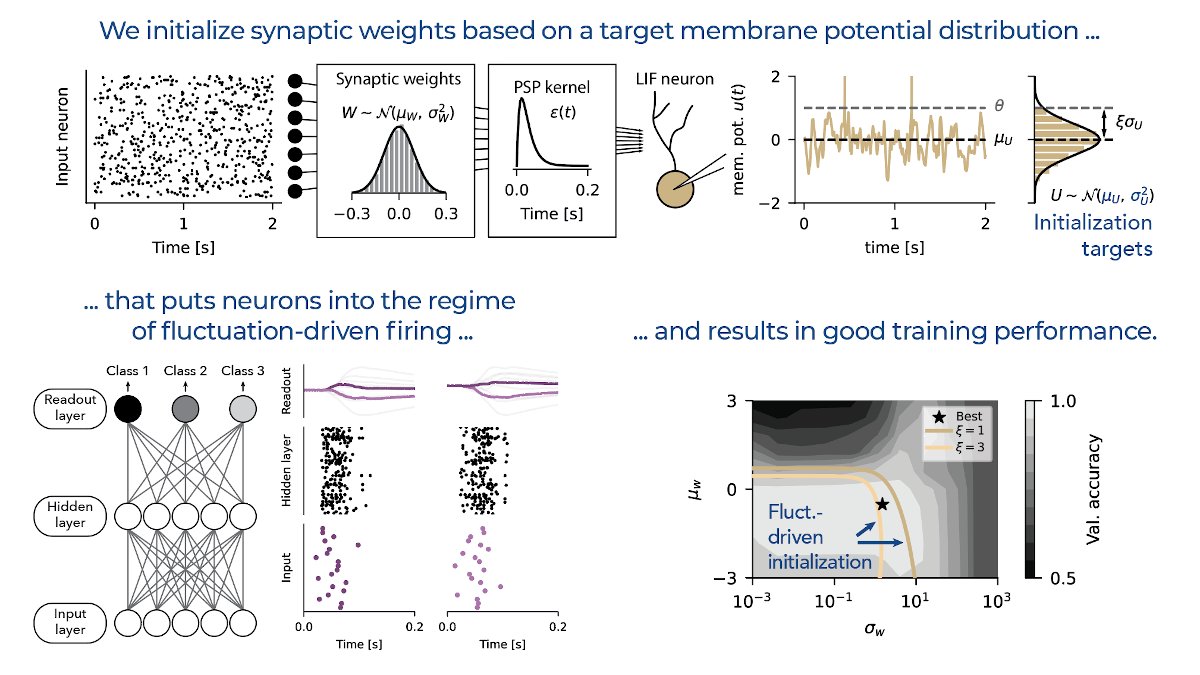
thumbnail

Training spiking neural networks (SNNs) to approximate complex functions is essential for studying information processing in the brain and neuromorphic computing. Yet, the binary nature of spikes constitutes a challenge for direct gradient-based training. To sidestep this problem, surrogate gradients (SGs) have proven empirically successful, but their theoretical foundation remains elusive. Here, we investigate the relation of SGs to two theoretically well-founded approaches. On the one hand, we consider smoothed probabilistic models, which, due to lack of support for automatic differentiation, are impractical for training deep SNNs, yet provide gradients equivalent to SGs in single neurons. On the other hand, we examine stochastic automatic differentiation, which is compatible with discrete randomness but has never been applied to SNN training. We find that the latter provides the missing theoretical basis for SGs in stochastic SNNs. We further show that SGs in deterministic networks correspond to a particular asymptotic case and numerically confirm the effectiveness of SGs in stochastic multi-layer SNNs. Finally, we illustrate that SGs are not conservative fields and, thus, not gradients of a surrogate loss. Our work provides the missing theoretical foundation for SGs and an analytically well-founded solution for end-to-end training of stochastic SNNs.

( paper | preprint | code )

Decoding finger velocity from cortical spike trains with recurrent spiking neural networks

Liu, Tengjun*; Gygax, Julia*; Rossbroich, Julian*; Chua, Yansong; Zhang, Shaomin & Zenke, Friedemann. (* equal contribution)
arXiv, 2024

thumbnail

Invasive cortical brain-machine interfaces (BMIs) can significantly improve the life quality of motor-impaired patients. Nonetheless, externally mounted pedestals pose an infection risk, which calls for fully implanted systems. Such systems, however, must meet strict latency and energy constraints while providing reliable decoding performance. While recurrent spiking neural networks (RSNNs) are ideally suited for ultra-low-power, low-latency processing on neuromorphic hardware, it is unclear whether they meet the above requirements. To address this question, we trained RSNNs to decode finger velocity from cortical spike trains (CSTs) of two macaque monkeys. First, we found that a large RSNN model outperformed existing feedforward spiking neural networks (SNNs) and artificial neural networks (ANNs) in terms of their decoding accuracy. We next developed a tiny RSNN with a smaller memory footprint, low firing rates, and sparse connectivity. Despite its reduced computational requirements, the resulting model performed substantially better than existing SNN and ANN decoders. Our results thus demonstrate that RSNNs offer competitive CST decoding performance under tight resource constraints and are promising candidates for fully implanted ultra-low-power BMIs with the potential to revolutionize patient care.

( | preprint | code )

Fluctuation-driven initialization for spiking neural network training

Rossbroich, Julian*, Gygax, Julia*, & Zenke, Friedemann. (* equal contribution)
Neuromorphic Computing and Engineering, 2022

thumbnail

Spiking neural networks (SNNs) underlie low-power, fault-tolerant information processing in the brain and could constitute a power-efficient alternative to conventional deep neural networks when implemented on suitable neuromorphic hardware accelerators. However, instantiating SNNs that solve complex computational tasks in-silico remains a significant challenge. Surrogate gradient (SG) techniques have emerged as a standard solution for training SNNs end-to-end. Still, their success depends on synaptic weight initialization, similar to conventional artificial neural networks (ANNs). Yet, unlike in the case of ANNs, it remains elusive what constitutes a good initial state for an SNN. Here, we develop a general initialization strategy for SNNs inspired by the fluctuation-driven regime commonly observed in the brain. Specifically, we derive practical solutions for data-dependent weight initialization that ensure fluctuation-driven firing in the widely used leaky integrate-and-fire neurons. We empirically show that SNNs initialized following our strategy exhibit superior learning performance when trained with SGs. These findings generalize across several datasets and SNN architectures, including fully connected, deep convolutional, recurrent, and more biologically plausible SNNs obeying Dale’s law. Thus fluctuation-driven initialization provides a practical, versatile, and easy-to-implement strategy for improving SNN training performance on diverse tasks in neuromorphic engineering and computational neuroscience.

( paper | preprint | code )